Unión
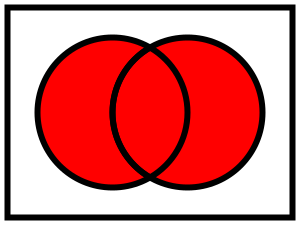
Diagrama de Venn que ilustra 
Para cada par de conjuntos A y B existe un conjunto que se denota como  el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como  de manera que sus elementos son todos los de manera que sus elementos son todos los  tales que tales que  . De esta manera . De esta manera  es el caso especial donde es el caso especial donde  . .
Es claro que el hecho de que un elemento x pertenezca a  es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir
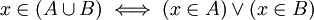
Ejemplos: si tenemos los conjuntos
  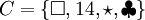 
Entonces
    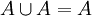
Intersección
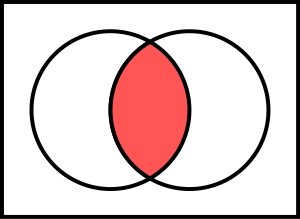
Diagrama de Venn que ilustra 
Los elementos comunes a  y y  forman un conjunto denominado intersección de forman un conjunto denominado intersección de  y y  , representado por , representado por  . Es decir, . Es decir,  es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B: es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
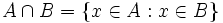 . .
Si dos conjuntos  y y  son tales que son tales que 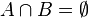 , entonces , entonces  y y  se dice que son conjuntos disjuntos. se dice que son conjuntos disjuntos.
Es claro que el hecho de que 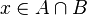 es condición necesaria y suficiente para afirmar que es condición necesaria y suficiente para afirmar que  y y 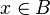 . Es decir . Es decir

Ejemplos: si tenemos los conjuntos
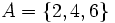  
Entonces:
  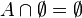 
Diferencia
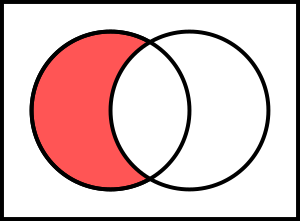 que muestra B − A que muestra B − A
Los elementos de un conjunto  que no se encuentran en otro conjunto que no se encuentran en otro conjunto  , forman otro conjunto llamado diferencia de , forman otro conjunto llamado diferencia de  y y  , representado por , representado por  . Es decir: . Es decir:
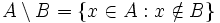 . .
o dicho de otra manera:
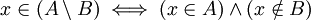
Algunas personas prefieren denotar la diferencia de  y y  como como  . .
Una propiedad interesante de la diferencia es que

eso es porque
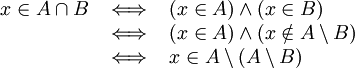
Ejemplos: Sin importar cual conjunto A elija usted, siempre se cumple
  
Complemento
El complemento de un conjunto A, es el conjunto de los elementos que pertenecen a algún conjunto U pero no pertenecen a A, que lo representaremos por 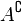 . Es decir . Es decir

El conjunto complemento siempre lo es respecto al conjunto universal que estamos tratando, esto es, si hablamos de números enteros, y definimos el conjunto de los números pares, el conjunto complemento de los números pares, es el formado por los números no pares. Si estamos hablando de personas, y definimos el conjunto de las personas rubias, el conjunto complementario es el de las personas no rubias.
En vista de que  y y  , entonces , entonces
 , ,
de manera que
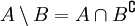
Pero también

de modo que

Diferencia simétrica
Los elementos de dos conjuntos,A y B a excepción de aquellos que se encuentran en el área de intersección de dichos conjuntos se define la diferencia simétrica.

|